Puissance en cyclisme sur route
Théorie
Formule générale
La puissance totale développée par un cycliste équilibre les pertes, selon la formule Puissance = 1/η.(PA + PEP + PRS + PRR) avec:
- 1/η: pertes dans la chaine de transmission
- PA: pertes aérodynamiques, prépondérantes sur le plat
- PEP: pertes dues au gain d'énergie potentielle, prépondérante en montée
- PRS: pertes dues au roulement au sol
- PRR: pertes dues à la rotation des roues, négligeables
Efficacité de la chaine de transmission η = 97,7%
Pertes aérodynamiques PA = 1/2.ρ.(CC + CR).VS.(VS + VV.cos(α))2
Les pertes aérodynamiques dépendent de
- ρ [kg/m3]: densité de l'air qui dépend de l'altitude et de la température, selon la formule de R02
 avec T température de l'air en °C et h altitude en mètres.
avec T température de l'air en °C et h altitude en mètres.
- VS [m/s]: vitesse par rapport au sol
- VV [m/s]: vitesse du vent
- α : angle entre la direction du vent et la direction de déplacement
et des coefficients
- CC [m²]: coefficient de frottement de l'air par rapport au cycliste, rigoureusement dans la direction de l'air, donc dépend de la direction du vent par rapport à la trajectoire. Il dépend donc de la position sur le vélo: redressé, mains en haut du guidon; baissé, mains en bas du guidon, dos arrondi... donné à 0,2565 m² dans R01
- CR [m²]: coefficient aérodynamique de rotation des roues à rayons donné à 0,0044 m² dans R01

Pertes dues à l'énergie potentielle PEP = VS.m.g.sin(β)
Les pertes dues au gain d'énergie potentielle dépendent de
- VS [m/s]: vitesse par rapport au sol
- m [kg]: masse totale en mouvement = masse du cycliste + vêtements + équipement + vélo + bidons...
- g [m/s²]: pesanteur = 9,81 m/s²
- β : angle entre la route et l'horizontale = arctangente ( dénivelé / distance)
Ces pertes sont majoritaires dés 4% de pente et presque exclusives pour une pente > 10%.
Pertes dues au roulement au sol PRS = VS.CRS.m.g.cos(β)
Les pertes dues au roulement au sol dépendent de
- VS [m/s]: vitesse par rapport au sol
- CRS coefficient de frottement au sol, dépend de la taille des pneus, de leur pression et de la rugosité du sol
- m [kg]: masse totale en mouvement = masse du cycliste + vêtements + équipement + vélo + bidons...
- g [m/s²]: pesanteur = 9,81 m/s²
- β : angle entre la route et l'horizontale = arctangente ( dénivelé / distance)
Résistance de roulement des pneus, selon R04
Le coefficient de résistance au roulement est le produit d'un coefficient lié à la surface par un coefficient lié au pneu. Celui ci est normalisé à 1 pour un pneu premimu gonflé à 120 PSI. Impact de la surface:
- piste en bois 0,001
- béton lisse 0,002
- route goudronnée 0,004
- route rugueuse 0,008
| Clincher | 50 PSI | 101 PSI | 120 PSI | 150 PSI |
|---|---|---|---|---|
| 3,45 bar | 7 bar | 8,28 bar | 10,35 bar | |
| Premimum | 1,70 | 1,09 | 1,00 | 0,94 |
| Utility | 2,17 | 1,42 | 1,28 | 1,13 |
| Touring | 2,63 | 1,75 | 1,56 | 1,33 |
- pneu course, gonflé à 8 bar, sur bonne route goudronnée CRR = 0,004
- pneu course, gonflé à 7 bar, sur route goudronnée moyenne CRR = 0,005
- pneu utility, gonflé à 7 bar, sur route goudronnée moyenne CRR = 0,006
- pneu touring, gonflé à 3,5 bar, sur mauvaise route CRR = 0,021
Pertes dues à la rotation des roues PRR = VS.(91+8,7.VS).10-3
Formule empirique basée sur des mesures de R01 En pratique ce terme est négligeable (2W à 40km/h).
Exemples de puissances pour différentes pentes et vitesses

Sensibilités du modèle
Sensibilités en montée: masse de 75 kg, pente de 8%, VS = 15 km/h
sensibilité à la masse sensibilité à la vitesse sensibilité à la pente
± 3 W / kg ± 20 W / (km/h) ± 31W / %
Sensibilités à plat: masse de 75 kg, pente de 0%, VS = 40 km/h
sensibilité au vent de face
± 11 W / (km/h)
Sensibilités du modèle: masse de 75 kg, pente de 0%, VS = 40 km/h, P = 253 W
sensibilité au coefficient aérodynamique du cycliste sensibilité au coefficient aérodynamique des roues sensibilité au coefficient de résistance du roulement au sol sensibilité à l'efficacité de la chaîne de transmission
± 9 W / 0,1 m² ± 9 W / 0,01 m² ± 8 W / 0,001 ± 3 W / %
Dénivelé horaire
Le tableau ci-contre donne la puissance nécessaire pour atteindre un certain dénivelé horaire, selon la pente.
Donc plus c'est raide... plus c'est facile de faire du dénivelé horaire!

Exemples
Ascension longue
Ascension du plateau de Beille, Ariège, +1 250m, 16km
Paramètres de calcul
Paramètres de l'ascension
Paramètres du jour
Paramètres du cycliste
Résultats du modèle
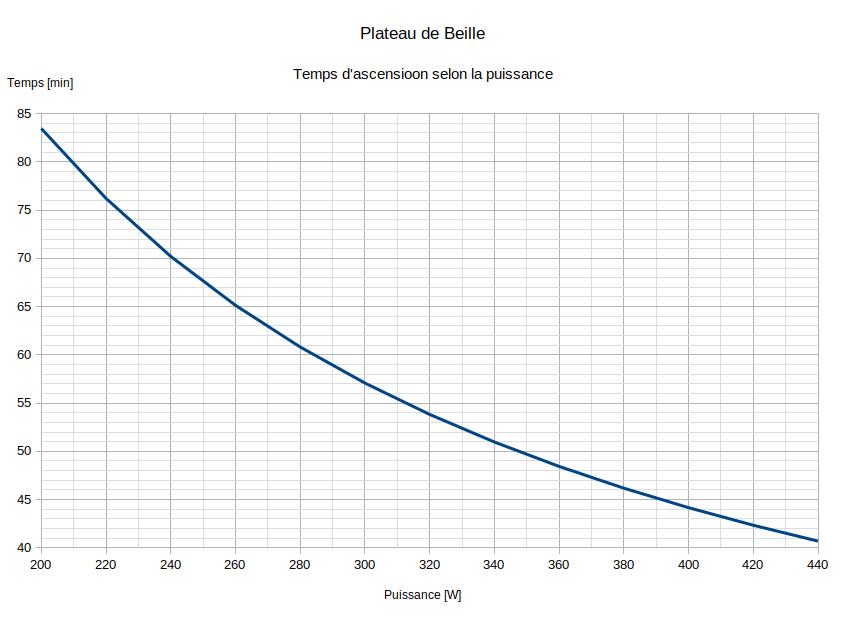
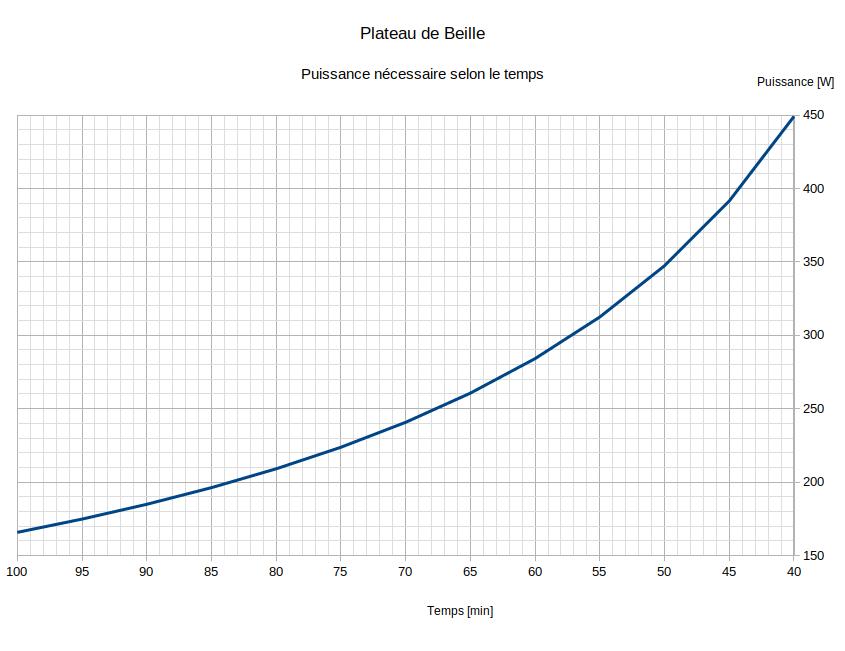
Ascension courte
Montée à la station de Bonascre, Ariège, +667m, 8,3km
Paramètres de calcul
Paramètres de l'ascension
Paramètres du jour
Paramètres du cycliste
Résultats du modèle
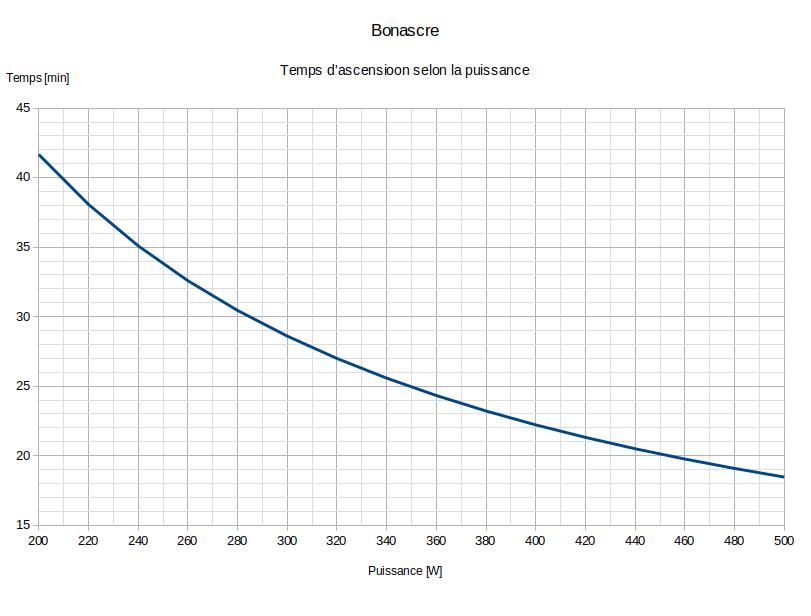
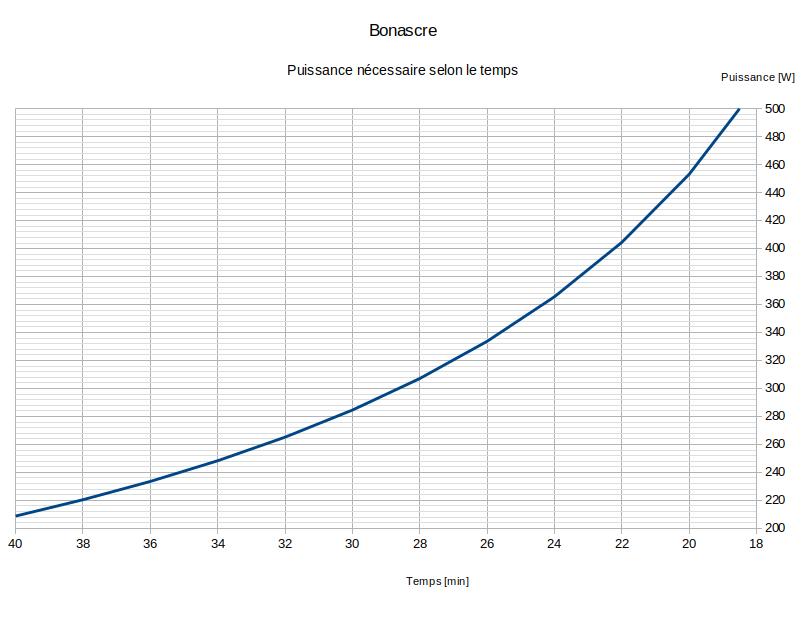
Références
- R01: Validation of a mathematical model for road cycling power, Martin Milliken Cobb McFadden Coggan, Journal of applied biomechanics, 1998
- R02: https://fr.wikipedia.org/wiki/Atmosphère_normalisée
- R03: https://www.chronoswatts.com/simulateur/1
- R04: https://analyticcycling.com/ForcesTire_TireRollingResistance.html
- R05: https://fr.wikipedia.org/wiki/%C3%89quation_cubique